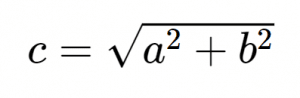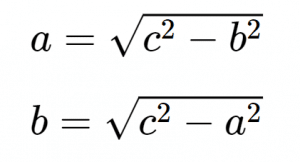Teorema di Pitagora online - Calcolo ipotenusa e cateti - Formula
Il miglior calcolatore del Teorema di Pitagora online
La calcolatrice che mettiamo a tua disposizione è un ottimo tool per risolvere problemi legati al Teorema di Pitagora.
Con questa calcolatrice puoi:
Trovare un cateto avendo l’ipotenusa e un cateto
Calcolare l’ipotenusa avendo i cateti
Calcolare l’area del triangolo rettangolo
Per utilizzare questo Calcolatrice del Teorema di Pitagora è necessario eseguire i seguenti passaggi:
- Seleziona il lato che vuoi calcolare
- Immettere i valori noti nella calcolatrice
- Premere il pulsante “Calcola”
La calcolatrice fornisce una soluzione dettagliata passo passo e genera una rappresentazione grafica del triangolo rettangolo dai dati forniti.
Ecco tutto ciò che devi sapere sul teorema di Pitagora:
Enunciato del Teorema
Il teorema di Pitagora afferma che se un triangolo ha un angolo retto, allora il quadrato del lato più lungo, chiamato ipotenusa, è uguale alla somma dei quadrati delle lunghezze dei due lati rimanenti, chiamati cateti.
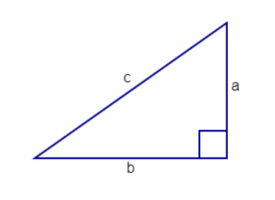
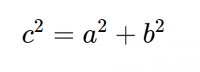
Grazie al teorema di Pitagora possiamo calcolare la lunghezza di tutti i lati di un triangolo rettangolo.
Il calcolo dell’ipotenusa viene effettuato con la seguente formula:
Le formule per il calcolo della misura dei cateti:
Dimostrazione teorema di Pitagora
Di seguito viene presentata una dimostrazione algebrica del teorema di Pitagora:
Il diagramma seguente mostra quattro triangoli rettangoli i cui lati sono a, b e c.
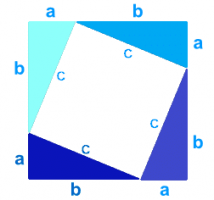
Ogni lato del quadrato presentato in figura ha una lunghezza di a + b, per cui per calcolare la sua area avremo:
A = (a + b) (a + b)
Ora procediamo a calcolare l’area di ciascuno dei pezzi nella figura.
- L’area della piazza centrale è pari a c2
- L’area di ogni triangolo è (ab/2)
- Aggiungendo le aree dei quattro triangoli che abbiamo (2ab)
Se aggiungiamo l’area di tutti i pezzi che compongono il quadrato, allora abbiamo
A = c 2 + 2ab