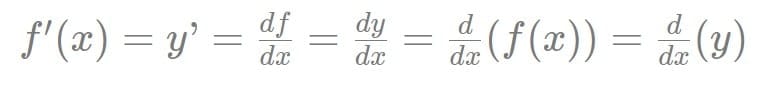Calcolatore Derivate - Calcolo derivate online e tabella delle derivate
Nelle tue mani mettiamo un ottimo Calcolatore di derivate online con passaggi. Indubbiamente questo è il miglior calcolatore per eseguire il calcolo derivate online. Oltre al calcolatore derivate online, spieghiamo tutti i concetti di base necessari per imparare a derivare le funzioni.
Calcolatore derivate online
Soluzione
In lavorazione...

-
Passo
-
Istruzioni per l'utilizzo del Calcolatore Derivate online
Usare il calcolatore di derivate online è molto semplice, devi solo entrare nella funzione che vuoi derivare e poi premere il pulsante “Calcola”. Di seguito sono riportati i comandi e gli operatori da utilizzare con questo risolutore di derivati:
| Funzioni | Descrizione |
| sin() | Seno |
| cos() | Coseno |
| tan() | Tangente |
| cot() | Cotangente |
| sec() | Secante |
| cosec() | Cosecante |
| sinh() | Seno iperbolico |
| cosh() | Coseno iperbolico |
| tanh() | Tangente iperbolica |
| coth() | Cotangente iperbolica |
| sech () | Secante iperbolica |
| csch() | Cosecante iperbolica |
| arcsin() | Arcoseno |
| arccos() | Arcocoseno |
| arctan() | Arcotangente |
| arccot() | Arcocotangente |
| arcsec() | Arcosecante |
| arccosec() | Arcocosecante |
| abs() | Valore assoluto |
| e | Numero di Nepero |
| ln() | Logaritmo naturale |
| lg() | Logaritmo in base 10 |
| ^ | Potenza |
| sqrt() | Radice quadrata |
| pi | 3.1416… |
Definizione di derivata
La derivata di una funzione può essere definita come il tasso di variazione di una funzione rispetto a una variabile indipendente. La derivata è uno dei pilastri fondamentali della matematica.
La derivata di f(x) rispetto a x è la funzione f'(x) ed è definita come:
\Large{f'(x)=\lim\limits_{h \to 0}\frac{f(x+h)-f(x)}{h}}
La notazione delle derivate
Ecco tutte le notazioni per rappresentare la derivata di una funzione:
Regole di derivazione - Come fare le derivate
Il calcolo delle derivate di funzioni utilizzando la formula derivativa generale può essere un processo complesso e noioso per determinate funzioni. Sebbene tu possa sempre utilizzare il calcolatore di derivate online, è importante che tu sappia come utilizzare le regole di derivazione principale, in modo da poter creare derivati in modo più semplice.
Ecco le regole di derivazione di base:
Derivata di una costante | Derivata di un numero
Se c è una costante e f(x) = c, allora f'(x) = 0.
Derivata del prodotto di una costante per una funzione
La derivata del prodotto di una costante `c` e di una funzione` f (x)` è uguale alla moltiplicazione della costante per la derivata della funzione.
Per p (x) = c * f (x), abbiamo p'(x) = c*f'(x).
Derivata di una somma/differenza di funzioni
La derivata della somma o differenza `p (x) = f (x) + – g (x)` è uguale alla somma delle derivate di ciascuna funzione, `p'(x) = f'(x) + – g(x)`.
Derivata di un prodotto di funzioni
A differenza di quanto accade nella derivata di una somma o differenza di funzioni, la derivata di un prodotto di due funzioni non è il prodotto delle derivate delle funzioni. La regola del prodotto afferma che la derivata di `p(x) = f(x)*g(x)` è uguale a `g(x)` moltiplicata per la derivata di `f'(x)` + `f (x)` moltiplicata per la derivata di `g'(x)`.
`p'(x) = g(x)*f'(x) + f(x)*g'(x)`.
Derivata di un rapporto di funzioni
La regola della derivata di un rapporto afferma che per una funzione `j(x) = f(x)/(g(x))` abbiamo che la sua derivata è:
`j'(x)=\frac{f'(x)g(x)-g'(x)f(x)}{(g(x))^2}`
Derivata esponenziale
Data una funzione esponenziale `f (x) = a^x`, la sua derivata viene calcolata come segue:
`f'(x)=a^x \cdot \ln(a)`
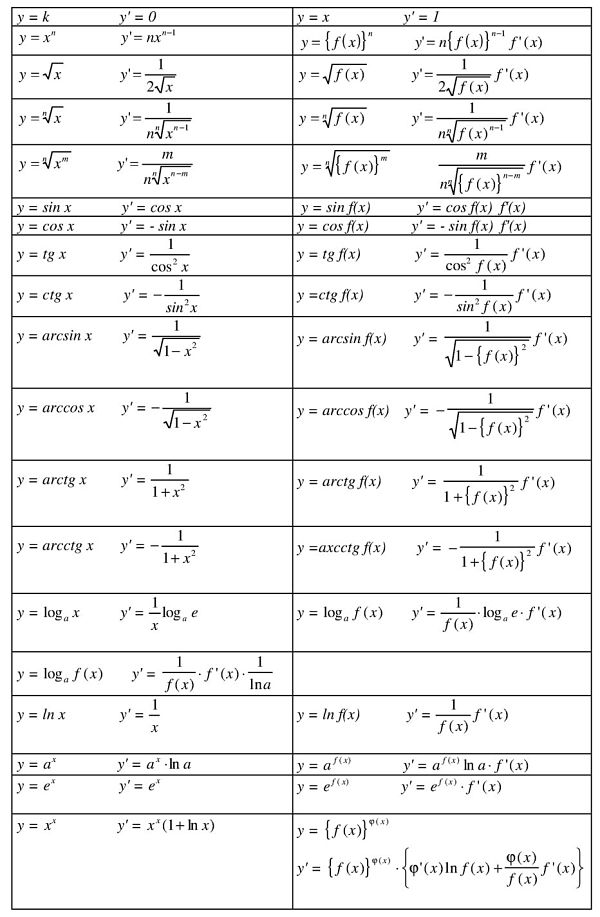
Tabella delle derivate